【線形代数学入門】行列の階数

1. 記事の目的
以下の記事で、行列の基本変形に関して述べた。本記事では基本変形を利用して、行列の階数という概念を導入する。行列の回数を導入すると、連立方程式が解けるための条件を記述することができる。

camelsan.hatenablog.com

2. 定理
行列の階数を導入するために、まず次の定理を証明する。

任意の $(m,n)$ 型行列 $A$ は、基本変形を何回か行うことで、次の標準形に変形される。

$F_{m,n}(r)=\begin{pmatrix}E_r&0_{r,m-r}\\0_{m-r,r}&0_{m-r,n-r}\end{pmatrix}$

$F_{m,n}(r)$ は図１のような行列である。

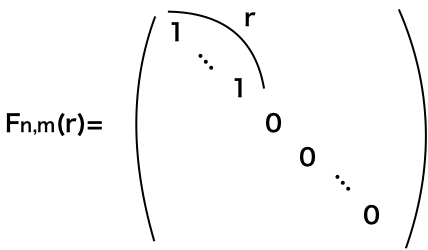
f:id:camelsan:20210207164641p:plain — 図１行列の標準形

対角線に並ぶ $1$ の数は $r$ は、 $A$ のみにより決まり、基本変形の仕方にはよらない。
証明： $A=0$ ならば、 $F_{m,n}(0)=0$ より、 $A$ はすでに標準形である。 $A\neq 0$ ならば、 $A$ の少なくとも一つの成分で $0$ でないものがあるので、基本変形を行うことで、 $(1,1)$ 成分に $0$ でない成分を移動させることができる。 $(1,1)$ をかなめとして、第１列、第一行を吐き出せば、

\begin{pmatrix}1&0&\dots&0\\0&&&\\\vdots&&*&\\0&&&\end{pmatrix}

の形になる。行列の掃き出しに関しては以下の記事を参照。

camelsan.hatenablog.com

ここで、第１行及び第１列以外の全てが $0$ であれば、 $F_{m,n}(1)$ の標準形となり、定理が成立する。もし、第１行及び第１列以外に、 $0$ でない成分があれば、その成分を基本変形により、 $(2,2)$ 成分に移し、 $(2,2)$ 成分をかなめとして、第２列と第２行を掃き出すと、

\begin{pmatrix}1&0&\dots&0\\0&1&\dots&0\\0&0&&\\ \vdots&\vdots&*&\\0&0&&\end{pmatrix}

の形に変形される。この操作を可能な限り続ければ、行列の大きさは有限なので、ある $r$ に関して、 $F_{m,n}(r)$ の形になる。
次に、 $r$ が(基本変形によらず)一意に決まることを示す。 $A$ が２通りの形、 $F(r)=F_{m,n}(r)$ 、 $F(s)=F_{m,n}(s)$ と変形されたと仮定する( $r\neq s$ )。ここで、 $r$ 、 $s$ のいずれかが小さいので、小さい方を $r$ とすれば、一般性を失わず $r\le s$ と仮定できる。 $A$ は $F(r)$ と $F(s)$ に変形されるので、ある正則行列 $P_1$ 、 $Q_1$ 、 $P_2$ 、 $Q_2$ があって、

$P_1AQ_1=F(r)$

$P_2AQ_2=F(s)$

よって、

$A=P_1^{-1}F(r)Q_1^{-1}$

$A=P_2^{-1}F(s)Q_2^{-1}$

と変形されるので、

$P_1^{-1}F(s)Q_1^{-1}=P_2^{-1}F(r)Q_2^{-1}$

となり、

$F(s)=P_1P_2^{-1}F(r)Q_2^{-1}Q_1$

となる。即ち、 $P=P_2^{-1}P_1$ 、 $Q=Q_2^{-1}Q_1$ とおくと、正則行列 $P$ 、 $Q$ を使って

$F(s)=PF(r)Q$

と表せる。 $P$ 、 $Q$ の行と列を $r$ 番目で四つに対称に区分けをして、

$P=\begin{pmatrix}P_{11}&P_{12}\\P_{12}&P_{22}\end{pmatrix}, Q=\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}$

とすれば( $P_{11}$ 、 $Q_{11}$ は $(r,r)$ 型行列)、

$\begin{split}F(s)&=\begin{pmatrix}P_{11}&P_{12}\\P_{12}&P_{22}\end{pmatrix}\begin{pmatrix}E_r&0\\0&0\end{pmatrix}\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}\\&=\begin{pmatrix}P_{11}&0\\P_{12}&0\end{pmatrix}\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}\\&=\begin{pmatrix}P_{11}Q_{11}&P_{11}Q_{12}\\P_{21}Q_{21}&P_{21}Q_{22}\end{pmatrix}\end{split}\tag{1}$

$r\le q$ の仮定により

$P_{11}Q_{11}=E_r\tag{2}$

$P_{11}Q_{12}=O_{r,m-r}\tag{3}$

$P_{21}Q_{11}=O_{m-r,r}\tag{4}$

が成り立つ(図２参照)。

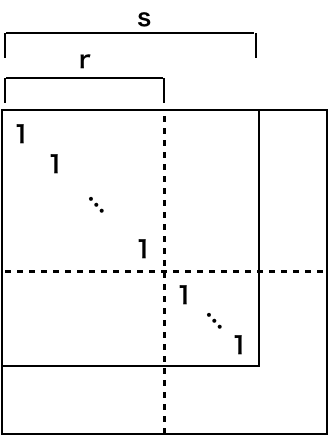
f:id:camelsan:20210208201916p:plain — 図２ (1)の参照図

以下の記事の正則行列に関する定理より、 $P_{11}$ 、 $Q_{11}$ は正則である。

camelsan.hatenablog.com

従って、(3)、(4)より、

$Q_{12}=P_{11}^{-1}O_{r,m-r}=O_{r,m-r}$

$P_{21}=O_{m-r,r}Q_{11}^{-1}=O_{m-r,r}$

よって、 $P_{21}Q_{12}=O_{m-r,n-r}$ となる。従って、(1)は、

$F(s)=\begin{pmatrix}E_r&0\\0&0\end{pmatrix}$

となり、これは $r=s$ でなければ成立しない。

3. 行列の階数
2.の定理で定まる、行列 $A$ に対する数、 $r$ を行列 $A$ の階数という。 $r$ は定理に示されているように、行列 $A$ だけで、一意に決定される。
例：次の行列 $A$ の階数を求める。

$A=\begin{pmatrix}2&1&3\\4&2&6\end{pmatrix}$

$\begin{split}A&\rightarrow\begin{pmatrix}2&1&3\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１行目のー２倍を第２行目に加える})\\&\rightarrow\begin{pmatrix}2&0&3\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１列目の-1/2倍を第２列目に加える})\\&\rightarrow\begin{pmatrix}2&0&0\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１列目の-3/2倍を第3列目に加える})\\&\rightarrow\begin{pmatrix}2&0&0\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１行目を1/2倍する})\end{split}$