この1年の変化は世間的にも、自分自身にとっても凄まじい変化の年だった。某ウイルスに対する変化に関してはもううんざりとするほど多くの人が感じています。なので、ここでは私自身の「生きやすさ」という価値観の変化に関して述べたいと思う。

早速だが一昨年1年間私は心の体調を崩し、ずっと臨床心理士の元、カウンセリングを受け続けていた(コロナが流行る前の年です)。まあ遅かれ早かれ、いずれはこうなっていたんだと思う。私は昔から、人を大事にして人に合わせて人に好かれることで生きやすくなるんだと思っていた。

苦手な陽気な大学生のノリに無理やり合わせたり、キャラがあまりなかったために、無理やり自分にキャラ付けをしてそれを自分に強いていた。そうしなければ、この先社会で生きていくのは無理なんだと思っていた。

カウンセリングの甲斐もあって、なんとか就職することはできた。カウンセリングや、就職活動、自分で心理学を勉強するうちに、人に合わせる必要なんてないんじゃないかと思うようになってきた。自分が思ったままに行動してもいいんじゃないかと。

就職をし、地元を離れ、このご時世もあって、昔に関わっていた人とは、もはや会うことは無くなった。このタイミングで電話帳の登録を家族以外全て削除した。そして人間関係は過剰に作らないようにしている。

社会人生活はというと、以前思っていた、人に合わせるのが重要だというのは全くなく、お互いが過剰にコミュニケーションを取るのではなく、良い距離感の職場だった(そのような雰囲気に適合していると見抜かれて採用されたのだろう)。ともかく、とても居心地の良いものだった。

この1年で「生きやすさ」の価値観は、人に合わせる、というものから、自分に素直になるというものに変化した。今は家族以外の人間関係を持たず、こんなふうに文章を書いたり、学生の時にはできなかったことを一人でやったり、一人考え事をする生活が大変幸せである(もちろん職場では仕事と割り切って、人間関係を築いているが…)。

「結婚が幸せ」という価値観があると思うが、私は全く思わない。誰かとずっと一緒にいるということを想像するだけで頭が割れるほど痛くなる(一緒にいて全く苦痛にならない人がもしも、いれば良いが…)。そんな調子だから、私は一生結婚しないだろう。

このご時世が明けて、多少は人と人の距離が近づくかもしれない。そうしたら今のあまり人と関わらなくても良い、という無くなるのかもしれない(飲み会にも行かなくてはならないかもしれない、昔の関わっていた人から連絡が来るかもしれない)。

しかし、そんな時でも自分に素直になり、関わりたければ、関わり、嫌だと思ったら、嫌だと言えるようになりたい。そのために今から心の準備をしている。

今、内気で悩んでいる人も、社会に出れば、その人に合った環境なんて無数に合って、明るいことなんてなんの取り柄にもならないことを伝えたい。むしろ社会に出てその心の内側にある、素晴らしいものが外に出ていくものです。内向的な人間が、優秀なことは心理学でも、たくさんの研究があります(それを聞いて自分も自信を持った)。

ゴチャゴチャと取り止めもないことを書いたけれど、私はこれからも自分の気持ちを大事にして、素直に生きてゆこうと思った。

2021-02-19

【Python入門】環境構築

Python

1. 記事の目的
本記事ではMac OSを用いて、Pythonでプログラミングを行うための環境構築に関して解説を行う。Mac OSではターミナルでlinuxコマンドを用いて開発ができる。またVisual Studio Codeをダウンロードしてエディタとしても扱える。本記事ではviエディターを使ってPythonのプログラムを書く方法を解説する。

本記事で使用した環境は以下の通りである。
macOS Catalina version 10.15.7
Python 3.8.5

2. ターミナル
まず、Pythonでプログラミングを行うために、ターミナルについて説明する。
次の手順でターミナルを開くことができる。

左下あたりにある「Finder」を開く。
図１ Finder
「ユーティリティ」というフォルダがあるので、開く。
図２ユーティリティ
「ターミナルが」あるので開く。
図３ターミナル

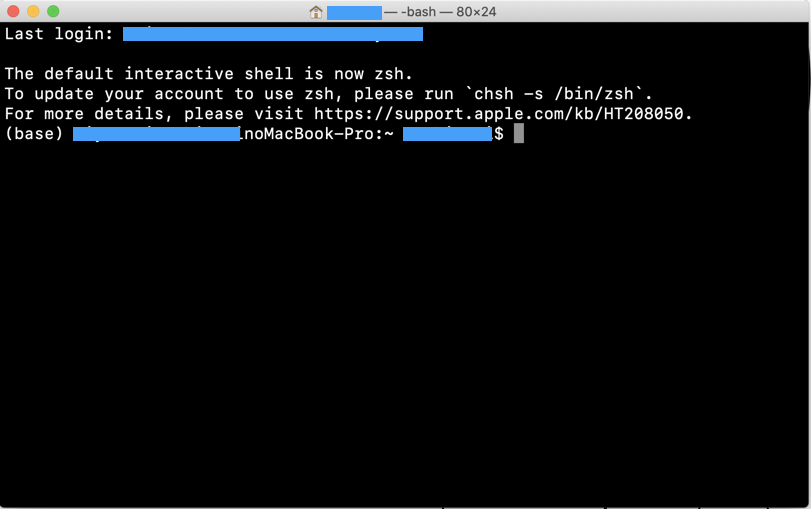
ターミナルを開くと、次のような画面が開かれる(青い四角で隠しているのは個人情報など)。

f:id:camelsan:20210219221715p:plain — 図４ターミナルの画面

2. Home brew
ターミナルから、Pythonをインストールするために、「Home brew」というソフトウェアを用いる。まず以下のサイトにアクセスする。

macOS（またはLinux）用パッケージマネージャー — Homebrew

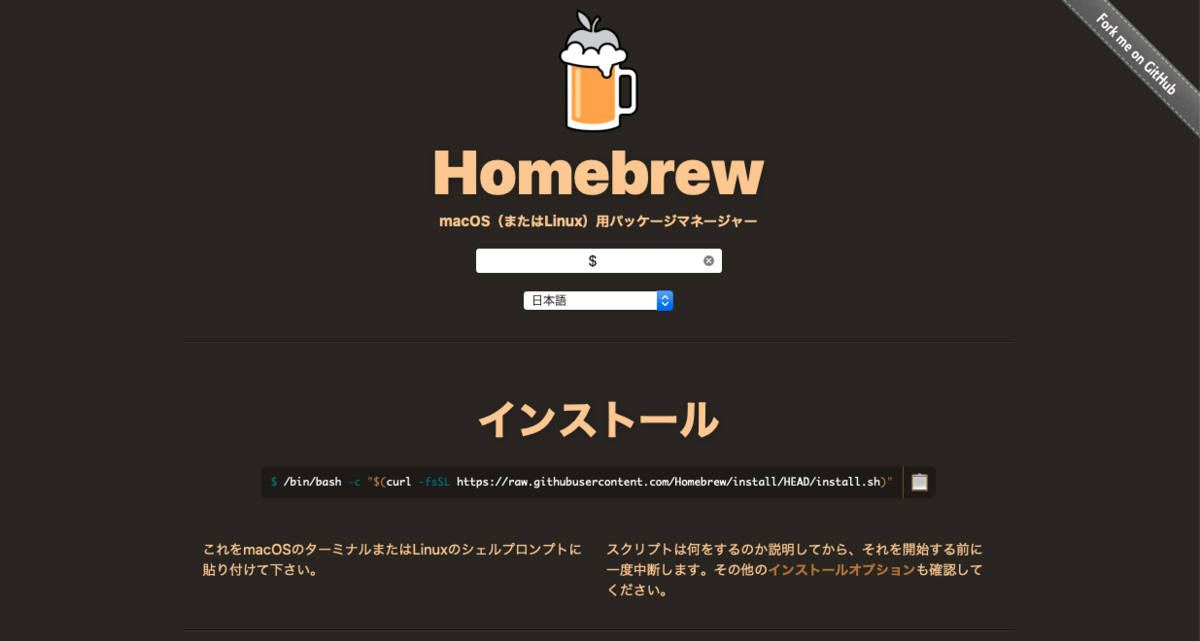
f:id:camelsan:20210219222543p:plain — 図５アクセス先の画面

画面の真ん中にあるコマンドをターミナルに貼り付けて、Enterを押す。

f:id:camelsan:20210219222930p:plain — 図６貼り付けた後の画面

3. Pythonのインストール
ターミナルに次のコマンドを入力する。

$ brew install python

これでPython3系がインストールされる。

4. Pythonインタプリンタ
ターミナル上で次のコマンドを入力することで、Pythonのインタプリンタを開くことができる。

$ python3

f:id:camelsan:20210219224124p:plain — 図７インタプリンタを開いた後の画面

インタプリンタとは、対話型のプログラミング方式である。つまり実行可能なコードを１行１行実行することができる。

インタプリンタを開いた後に、次を入力する。

>>>1+3

Enterを押すと、画面に

と表示される。つまり1+3が計算された。

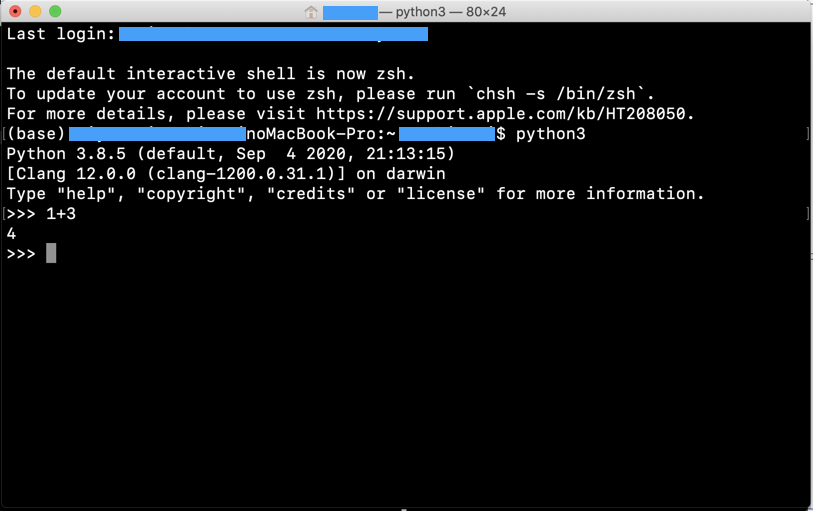
f:id:camelsan:20210219224619p:plain — 図８インタプリンタで計算

このように、インタプリンタを使用して、Pythonのプログラミングを行うことができる。インタプリンタを抜けるには次のコマンドを入力すれば良い。

>>>exit()

5. viエディター
原理的には、以上のようにでPythonのプログラミングを行うことができるが、１行１行入力して実行するのは面倒くさい(実際こんなやり方はしない)。動作確認の時に使用するくらいである。

一般的にはファイルにプログラムコードを書き、それ実行するというのが普通である。

プログラムは、エディターに書き込んで、Pythonファイルとして保存して、それ実行するという方式が取られる。そのためのエディターとして、viエディターというものを紹介する。

まず、ターミナルに次のコマンドを入力する。

$ vi hello.py

f:id:camelsan:20210219225833p:plain — 図９入力後の画面

これで、「hello.py」というPythonファイルが作成され、その中身が編集できるようになった。

「I」(キーボードのi)を入力することでviエディター内に文字を入力することができる(viエディターを開くたびにiを入力する必要がある)。

ファイルの中に次のコードを入力する。

print("Hello World")

f:id:camelsan:20210219230446p:plain — 図10 入力後の画面

入力後、「Esc」(エスケープキー)を入力する。そして、「:wq」(コロン+w+q)と入力して、エンターキーをおす(必ず半角にしてから入力)。

そうすると、元のターミナルの画面に戻ってくる。これでさきほど入力したコード(print("Hello World."))が記載されたPythonファイルが保存される。

f:id:camelsan:20210219231215p:plain — 図１１戻ってきた後の画面

6. Pythonコードの実行方法
viエディターで編集、保存したPythonファイルを用いてPythonコードを実行する方法を解説する。基本的には「python3 Pythonファイル名」と入力すれば実行することができる。実際に次のコマンドを打って先程のPythonファイル(hello.py)を実行してみる。

$ python3 hello.py

そうすると画面に

$ Hello World

と表示される。

f:id:camelsan:20210219231858p:plain — 図１２コマンド入力後の画面

Pythonのコードで、print("〜")は、かっこ内の文字列を画面に表示せよ、という命令なので、コードが正しく動いたということになる。

7. 参考文献
[1] Home brew
macOS（またはLinux）用パッケージマネージャー — Homebrew
[2] Quiita, "Home brewのインストール"
Homebrewのインストール - Qiita
Home brewのインストールに関しては、こちらを見た方がわかりやすいと思われる。
[3] Quiita, "Python3インストール（Mac編）"
Python3インストール（Mac編） - Qiita
Pythonのインストールで詰まったらこちらを参照すると良い。
[4] 詳細!Python3入門ノート

Pythonに関して、わかりやすく解説されている書籍。

2021-02-14

【線型代数学入門】逆行列の計算方法

線形代数

1. 記事の目的
以下の記事で逆行列に関して述べた。

camelsan.hatenablog.com

しかし、逆行列の具体的な計算方法を述べずにいた。ここで、以下の記事で行列の階数を導入した。行列の階数を使って逆行列を求める方法に関する定理を証明することができる。

camelsan.hatenablog.com

2. 結論
最初に、どのように逆行列が計算できるか結論を先に述べる。 $(n,n)$ 型正則行列 $A$ の逆行列 $A^{-1}$ を求めるには、 $(n,2n)$ 型行列

$\begin{pmatrix}A&E\end{pmatrix}\tag{1}$

を左基本変形のみで

$\begin{pmatrix}E&B\end{pmatrix}\tag{2}$

の形にしたとき、 $B$ が $A$ の逆行列である。即ち、 $B=A^{-1}$ である。左基本変形のみで、(1)式が(2)の形に必ず変形されることは、明らかではないが、次に証明する定理で保証される。

3. 定理
まず初めに次の定理を証明する。
定理[1]
$n$ 次正方行列 $A$ が正則であるためには、その階数が $n$ に等しいことが必要かつ十分な条件である。
証明： $A$ を基本変形して、ある正則行列 $P$ 、 $Q$ に対して、

$PAQ=\begin{pmatrix}E_r&0\\0&0\end{pmatrix}\tag{3}$

となったとする。 $A$ が正則であると仮定すると、 $PAQ$ も正則でなければならない。従って、(3)式より、 $r=n$ である。逆に、 $r=n$ と仮定する。

$PAQ=E_n$

より、 $A=P^{-1}Q^{-1}$ 。よって、 $A$ は正則である。

上記の定理を使って、次の定理を証明することができる。
定理[2]
行列 $A$ が正則ならば、左(あるいは右)基本変形だけで $A$ を単位行列に変形することができる。逆に、左(あるいは右)基本変形だけで $A$ を単位行列に変形できれば、 $A$ は正則である。
証明： $A$ が正則ならば、定理[1]より、ある正則行列 $P$ 、 $Q$ があって、

$PAQ=E\tag{4}$

( $P$ 、 $Q$ は基本行列の積)(4)式の左から $Q$ 、右から $Q^{-1}$ を掛けると、

$QPA=E\tag{5}$

$QP$ も基本行列の積なので、(5)式は、左基本変形のみで $A$ を単位行列に変形できることを示している。また、逆に $A$ が左基本行列のみで単位行列に変形できると仮定すると、基本行列の積である $Q$ が存在して、

$QA=E$

となる。これは、 $A$ の階数が、 $n$ であることを意味するので、定理[1]より $A$ は正則である。

4. 逆行列の計算方法
$A$ が正装行列のとき定理[2]から、左基本変形のみで、単位行列に変形できるので、ある正則行列 $Q$ があって、

$QA=E$

両辺に右から $A^{-1}$ を掛けると、

$Q=A^{-1}$

ここで、 $(n,2n)$ 型行列

$\begin{pmatrix}A&E\end{pmatrix}$

を考える。このとき $Q$ を左から掛けると、

$\begin{split}Q\begin{pmatrix}A&E\end{pmatrix}&=\begin{pmatrix}QA&QE\end{pmatrix}\ \ \ \ (\textbf{区分けされた行列の演算})\\&=\begin{pmatrix}E&A^{-1}\end{pmatrix}\end{split}$

即ち、本記事の冒頭で述べた事が言える。

5. 逆行列の計算例

$A=\begin{pmatrix}1&2&3\\-2&-3&-4\\2&2&4\end{pmatrix}$

の逆行列を求める。

$\begin{split}\begin{pmatrix}A&E\end{pmatrix}&=\begin{pmatrix}1&2&3&1&0&0\\-2&-3&-4&0&1&0\\2&2&4&0&0&1\end{pmatrix}\\&\rightarrow\begin{pmatrix}1&2&3&1&0&0\\0&1&2&2&1&0\\2&2&4&0&0&1\end{pmatrix}\ \ \ \ (\textbf{１行目の２倍を２行目に加える})\\&\rightarrow\begin{pmatrix}1&2&3&1&0&0\\0&1&2&2&1&0\\0&-2&-2&-2&0&1\end{pmatrix}\ \ \ \ (\textbf{１行目のー２倍を３行目に加える})\\&\rightarrow\begin{pmatrix}1&0&-1&-3&-2&0\\0&1&2&2&1&0\\0&-2&-2&-2&0&1\end{pmatrix}\ \ \ \ (\textbf{２行目のー２倍を１行目に加える})\\&\rightarrow\begin{pmatrix}1&0&-1&-3&-2&0\\0&1&2&2&1&0\\0&0&2&2&2&1\end{pmatrix}\ \ \ \ (\textbf{２行目の２倍を３行目に加える})\\&\rightarrow\begin{pmatrix}1&0&-1&-3&-2&0\\0&1&2&2&1&0\\0&0&1&1&1&\frac{1}{2}\end{pmatrix}\ \ \ \ (\textbf{３行目を1/2倍})\\&\rightarrow\begin{pmatrix}1&0&0&-2&-1&\frac{1}{2}\\0&1&2&2&1&0\\0&0&1&1&1&\frac{1}{2}\end{pmatrix}\ \ \ \ (\textbf{３行目を１行目に加える})\\&\rightarrow\begin{pmatrix}1&0&0&-2&-1&\frac{1}{2}\\0&1&0&0&-1&-1\\0&0&1&1&1&\frac{1}{2}\end{pmatrix}\ \ \ \ (\textbf{３行目の−２倍を２行目に加える})\end{split}$

よって、

$A^{-1}=\begin{pmatrix}-2&-1&\frac{1}{2}\\0&-1&-1\\1&1&\frac{1}{2}\end{pmatrix}\$

となる。

camelsan.hatenablog.com

6. 参考文献
[1] 線型代数入門

線型代数入門（基礎数学） [ 斎藤正彦 ]

価格:2,090円
(2021/12/6 21:07時点)
感想(2件)

2021-02-08

【線形代数学入門】行列の階数

線形代数

1. 記事の目的
以下の記事で、行列の基本変形に関して述べた。本記事では基本変形を利用して、行列の階数という概念を導入する。行列の回数を導入すると、連立方程式が解けるための条件を記述することができる。

camelsan.hatenablog.com

2. 定理
行列の階数を導入するために、まず次の定理を証明する。

任意の $(m,n)$ 型行列 $A$ は、基本変形を何回か行うことで、次の標準形に変形される。

$F_{m,n}(r)=\begin{pmatrix}E_r&0_{r,m-r}\\0_{m-r,r}&0_{m-r,n-r}\end{pmatrix}$

$F_{m,n}(r)$ は図１のような行列である。

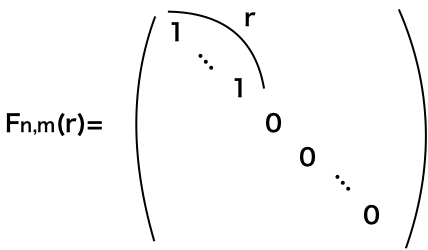
f:id:camelsan:20210207164641p:plain — 図１行列の標準形

対角線に並ぶ $1$ の数は $r$ は、 $A$ のみにより決まり、基本変形の仕方にはよらない。
証明： $A=0$ ならば、 $F_{m,n}(0)=0$ より、 $A$ はすでに標準形である。 $A\neq 0$ ならば、 $A$ の少なくとも一つの成分で $0$ でないものがあるので、基本変形を行うことで、 $(1,1)$ 成分に $0$ でない成分を移動させることができる。 $(1,1)$ をかなめとして、第１列、第一行を吐き出せば、

\begin{pmatrix}1&0&\dots&0\\0&&&\\\vdots&&*&\\0&&&\end{pmatrix}

の形になる。行列の掃き出しに関しては以下の記事を参照。

camelsan.hatenablog.com

ここで、第１行及び第１列以外の全てが $0$ であれば、 $F_{m,n}(1)$ の標準形となり、定理が成立する。もし、第１行及び第１列以外に、 $0$ でない成分があれば、その成分を基本変形により、 $(2,2)$ 成分に移し、 $(2,2)$ 成分をかなめとして、第２列と第２行を掃き出すと、

\begin{pmatrix}1&0&\dots&0\\0&1&\dots&0\\0&0&&\\ \vdots&\vdots&*&\\0&0&&\end{pmatrix}

の形に変形される。この操作を可能な限り続ければ、行列の大きさは有限なので、ある $r$ に関して、 $F_{m,n}(r)$ の形になる。
次に、 $r$ が(基本変形によらず)一意に決まることを示す。 $A$ が２通りの形、 $F(r)=F_{m,n}(r)$ 、 $F(s)=F_{m,n}(s)$ と変形されたと仮定する( $r\neq s$ )。ここで、 $r$ 、 $s$ のいずれかが小さいので、小さい方を $r$ とすれば、一般性を失わず $r\le s$ と仮定できる。 $A$ は $F(r)$ と $F(s)$ に変形されるので、ある正則行列 $P_1$ 、 $Q_1$ 、 $P_2$ 、 $Q_2$ があって、

$P_1AQ_1=F(r)$

$P_2AQ_2=F(s)$

よって、

$A=P_1^{-1}F(r)Q_1^{-1}$

$A=P_2^{-1}F(s)Q_2^{-1}$

と変形されるので、

$P_1^{-1}F(s)Q_1^{-1}=P_2^{-1}F(r)Q_2^{-1}$

となり、

$F(s)=P_1P_2^{-1}F(r)Q_2^{-1}Q_1$

となる。即ち、 $P=P_2^{-1}P_1$ 、 $Q=Q_2^{-1}Q_1$ とおくと、正則行列 $P$ 、 $Q$ を使って

$F(s)=PF(r)Q$

と表せる。 $P$ 、 $Q$ の行と列を $r$ 番目で四つに対称に区分けをして、

$P=\begin{pmatrix}P_{11}&P_{12}\\P_{12}&P_{22}\end{pmatrix}, Q=\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}$

とすれば( $P_{11}$ 、 $Q_{11}$ は $(r,r)$ 型行列)、

$\begin{split}F(s)&=\begin{pmatrix}P_{11}&P_{12}\\P_{12}&P_{22}\end{pmatrix}\begin{pmatrix}E_r&0\\0&0\end{pmatrix}\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}\\&=\begin{pmatrix}P_{11}&0\\P_{12}&0\end{pmatrix}\begin{pmatrix}Q_{11}&Q_{12}\\Q_{21}&Q_{22}\end{pmatrix}\\&=\begin{pmatrix}P_{11}Q_{11}&P_{11}Q_{12}\\P_{21}Q_{21}&P_{21}Q_{22}\end{pmatrix}\end{split}\tag{1}$

$r\le q$ の仮定により

$P_{11}Q_{11}=E_r\tag{2}$

$P_{11}Q_{12}=O_{r,m-r}\tag{3}$

$P_{21}Q_{11}=O_{m-r,r}\tag{4}$

が成り立つ(図２参照)。

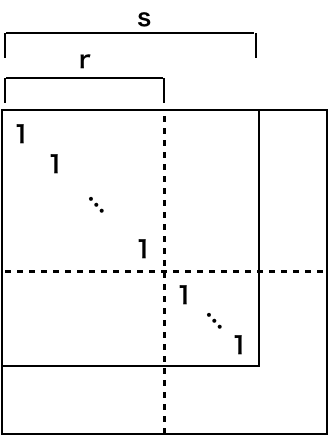
f:id:camelsan:20210208201916p:plain — 図２ (1)の参照図

以下の記事の正則行列に関する定理より、 $P_{11}$ 、 $Q_{11}$ は正則である。

camelsan.hatenablog.com

従って、(3)、(4)より、

$Q_{12}=P_{11}^{-1}O_{r,m-r}=O_{r,m-r}$

$P_{21}=O_{m-r,r}Q_{11}^{-1}=O_{m-r,r}$

よって、 $P_{21}Q_{12}=O_{m-r,n-r}$ となる。従って、(1)は、

$F(s)=\begin{pmatrix}E_r&0\\0&0\end{pmatrix}$

となり、これは $r=s$ でなければ成立しない。

3. 行列の階数
2.の定理で定まる、行列 $A$ に対する数、 $r$ を行列 $A$ の階数という。 $r$ は定理に示されているように、行列 $A$ だけで、一意に決定される。
例：次の行列 $A$ の階数を求める。

$A=\begin{pmatrix}2&1&3\\4&2&6\end{pmatrix}$

$\begin{split}A&\rightarrow\begin{pmatrix}2&1&3\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１行目のー２倍を第２行目に加える})\\&\rightarrow\begin{pmatrix}2&0&3\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１列目の-1/2倍を第２列目に加える})\\&\rightarrow\begin{pmatrix}2&0&0\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１列目の-3/2倍を第3列目に加える})\\&\rightarrow\begin{pmatrix}2&0&0\\0&0&0\end{pmatrix}\ \ \ \ (\textbf{第１行目を1/2倍する})\end{split}$

従って、 $A$ の階数は $1$ である。

camelsan.hatenablog.com

4. 参考文献
[1] 整形代数学入門

2021-02-06

【線形代数学入門】行列の掃き出し

線形代数

1. 記事の目的
以下の記事で、行列の基本変形に関して述べた。本記事では行列を用いて連立方程式を解く際の、行列の操作である掃き出しについて解説する。掃き出しの操作としては、行列の基本変形を繰り返して行われるものである。

2. 行列の掃き出し
$(m,n)$ 型行列 $A$ の $(p,q)$ 成分が $0$ でないとき、次の一連の操作を考える。
(1) $p$ 行を $(p,q)$ 成分で割って、 $(p,q)$ 成分を $1$ にする((左１)の操作)。
(2) $p$ 以外のすべての $i$ に対して、第 $i$ 行から第 $p$ 行の $(i,p)$ 成分倍を引く((左３)の操作)。

(1)、(2)の操作により $A$ は図１の $A^{\prime}$ に変形される。

f:id:camelsan:20210206101029p:plain — 図１第q列の掃き出し

これを $(p,q)$ をかなめとし、左から第 $q$ 列を掃き出すという。

さらに次の操作を行う。
(3) $q$ 以外の全ての $j$ に対し、第 $j$ 列から第 $q$ 列の $(p,j)$ 成分倍を引く。

(3)の操作により、 $A^{\prime}$ は図２の $A^{\prime\prime}$ に変形される。

f:id:camelsan:20210206101736p:plain — 図２第p行の掃き出し

3. 正則行列に関する定理
掃き出しを利用することで、正則行列に関する、次の定理を証明することができる。

$n$ 次正方行列 $A$ に対し、 $XA=E$ となる $n$ 次行列 $X$ が存在すれば、 $A$ は正則である。
( $A$ が正則であるかを判定するには、 $AX=XA=E$ となる行列 $X$ が存在するか否かを調べる必要があったが、 $XA=E$ となる $X$ を見つけるだけで良いことになる、というのがこの定理の意味することである。)
証明： $n$ に関する数学的帰納法により証明する。 $n$ が $1$ のとき、 $A$ と $X$ は共に通常の数となり、交換できるので、成立する。
$n>1$ とし、 $n-1$ 次行列に対しては主張が正しいと仮定する。行列に $(1,1)$ 成分を考える。その成分が $0$ でないときは良い。 $0$ のとき、 $A$ は零行列ではないので(零行列とすると、 $AX=E$ より、 $E=0$ となり矛盾)、どこかの成分は $0$ ではない成分がある。よって、行や列を入れ替えることで(基本変形を繰り返す)、 $(1,1)$ 成分に $0$ でない成分を移動させる。 $(1,1)$ をかなめとし、第 $1$ 列と第 $1$ 行を掃き出すと $A$ は次の行列 $B$ に変形される。

$\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&A_1\end{pmatrix}$

ここで、 $^{t}\textbf{0}=(0,\dots,0)$ を表す。
行列の基本変形とは、基本行列を掛けることなので、ある正則行列 $P$ 、 $Q$ を適当に取ると( $P, Q$ は基本行列をいくつか欠けたもの)

$PAQ=B=\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&A_1\end{pmatrix}$

が成り立つ。

ここで、 $X_1A_1=E$ となる $X_1$ が存在することを証明する。 $XA=E$ より、この式に $PAQ$ という項が現れるようにしたい。左から $Q^{-1}$ 、右から $Q$ を掛けると、

$Q^{-1}XAQ=QQ^{-1}=E$

$P^{-1}P=E$ より、

$E=Q^{-1}XEAQ=Q^{-1}XP^{-1}PAQ$

ここで出現する、未知の行列である、[texQ^{-1}XP^{-1}]について考える。 $Q^{-1}XP^{-1}$ を $PAQ$ と同じ形に区分けする。即ち、

$Q^{-1}XP^{-1}=\begin{pmatrix}u&^{t}\textbf{z}\\ \textbf{y}&X_1\end{pmatrix}$

とする。 $(Q^{-1}XP^{-1})(PAQ)=E$ より、

$\begin{pmatrix}u&^{t}\textbf{z}\\ \textbf{y}&X_1\end{pmatrix}\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&A_1\end{pmatrix}=\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&E_{n-1}\end{pmatrix}$

左辺を計算すると、

$\begin{pmatrix}u&^{t}\textbf{z}\\ \textbf{y}&X_1\end{pmatrix}\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&A_1\end{pmatrix}=\begin{pmatrix}u&^{t}\textbf{z}A_1\\ \textbf{y}&X_1A_1\end{pmatrix}$

より、

$\begin{pmatrix}u&^{t}\textbf{z}A_1\\ \textbf{y}&X_1A_1\end{pmatrix}=\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&E_{n-1}\end{pmatrix}$

従って、

X_1A_1=E_{n-1}

よって、帰納法の仮定より、 $A_1$ は正則である。従って以下の記事の区分けされた行列に関する逆行列の定理(左上と右下の行列が正則であれば、元の行列も正則)より

$B=\begin{pmatrix}1&^{t}\textbf{0}\\ \textbf{0}&A_1\end{pmatrix}$

も正則である。 $PAQ=B$ より、 $A=P^{-1}AQ^{-1}$ であるから、 $A$ も正則である(正則行列同士をかけても正則)。

camelsan.hatenablog.com

4. 参考文献
[1] 線形代数学入門

線型代数入門（基礎数学） [ 斎藤正彦 ]

価格:2,090円
(2021/12/6 21:07時点)
感想(2件)

2021-01-30

【線型代数学入門】基本変形

線形代数

1. 記事の目的
以下の記事で行列の演算に関して述べた。本記事では行列を利用した連立一次方程式の解法で必要となる基本変形に関して解説する。

camelsan.hatenablog.com

2. 基本変形
行列を扱う際、できるだけ簡単な形の行列に変形して考えることが有用な場合が多い。例えば連立一次方程式の開放に行列を利用するときも、そのひとつである。具体的には、

$\begin{pmatrix}0&2&4&2\\1&2&3&1\\-2&-1&0&1\end{pmatrix}$

のような行列を、

$\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\end{pmatrix}$

のような行列に変形する。

3. 基本行列
以下で基本行列と呼ばれる３種類の特別な正方行列を述べる。
(1)図１の行列を $P_n(i,j)$ とする。

f:id:camelsan:20210126203931p:plain — 図１基本行列一つ目

$n$ 次単位行列の、第 $i$ 列と第 $j$ 列を交換したものである。 $(m,n)$ 型行列 $A$ に対し、 $P_m(i,j)$ を左から掛けると、 $A$ の第 $i$ 行と第 $j$ 行が交換される。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, P_2(1,2)=\begin{pmatrix}0&1\\1&0\end{pmatrix}$

とする。このとき

$\begin{split}P_2(1,2)A&=\begin{pmatrix}0&1\\1&0\end{pmatrix}\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\\&=\begin{pmatrix}4&5&6\\1&2&3\end{pmatrix}\end{split}$

となる。従って、 $P_2(1,2)$ を左から掛けると、ちょうど $A$ の第 $i$ 行と第 $j$ 行が交換されている。

$(m,n)$ 型行列 $A$ に対し、 $P_n(i,j)$ を右から掛けると、 $A$ の第 $i$ 行と第 $j$ 列が交換される。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, P_3(1,2)=\begin{pmatrix}0&1&0\\1&0&0\\0&0&1\end{pmatrix}$

とする。このとき

$\begin{split}AP_3(1,2)&=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\begin{pmatrix}0&1&0\\1&0&0\\0&0&1\end{pmatrix}\\&=\begin{pmatrix}2&1&3\\5&4&6\end{pmatrix}\end{split}$

となる。従って、 $P_3(1,2)$ を右から掛けると、ちょうど、 $A$ の第 $1$ 列と第 $2$ 列が交換されている。

$P_n(i,j)$ は正則で、逆行列は $P_n(i,j)$ 自身である。
証明：逆行列の定義については次の記事を参考にしてほしい。

camelsan.hatenablog.com

$P_n(i,j)P_n(i,j)$ を考える。 $P_n(i,j)$ に右から $P_n(i,j)$ がかけられていると考えると、 $P_n(i,j)$ の第 $i$ 列と第 $j$ 列が交換されるので、これは単位行列 $E$ となる。従って、

$P_n(i,j)P_n(i,j)=E$

よって $P_n(i,j)$ は正則で、逆行列は $P_n(i,j)$ 自身である。

(2) 図２の行列を $Q_n(i;c)$ とする。

f:id:camelsan:20210127192413p:plain — 図２基本行列二つ目

単位行列の $(i,i)$ 成分を、 $0$ でない数 $c$ に置き換えた行列である。

$(m,n)$ 型行列 $A$ に対し、左から $Q_m(i;c)$ を掛けると、 $A$ の第 $i$ 行が $c$ 倍される。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, Q_2(1;2)=\begin{pmatrix}2&0\\0&1\end{pmatrix}$

とすると、

$Q_2(1;2)A=\begin{pmatrix}2&0\\0&1\end{pmatrix}\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}=\begin{pmatrix}2&4&6\\4&5&6\end{pmatrix}$

従って、 $Q_2(1;2)$ を左から掛けると、ちょうど $A$ の $1$ 行目が $2$ 倍されている。

$(m,n)$ 型行列 $A$ に対して右から $Q_n(i;c)$ を掛けると、 $A$ の第 $i$ 列が $c$ 倍される。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, Q_3(1;2)=\begin{pmatrix}2&0&0\\0&1&0\\0&0&1\end{pmatrix}$

とすると

$AQ_3(1;2)=\begin{pmatrix}2&2&3\\8&5&6\end{pmatrix}$

従って、 $Q_3(1;2)$ を右から掛けると、ちょうど $A$ の $1$ 列目が $2$ 倍されている。

$Q_n(i;c)$ は正則で、その逆行列は $Q_n(i;c^{-1})$ である。
証明： $Q_n(i;c)Q_n(i;c^{-1})$ を考える。 $Q_n(i;c)$ に右から $Q_n(i;c^{-1})$ がかけられていると考えると、 $Q_n(i;c)$ の第 $i$ 列が $c^{-1}$ されるので、単位行列となる。即ち

$Q_n(i;c)Q_n(i;c^{-1})=E$

$Q_n(i;c^{-1})Q_n(i;c)$ を考える。 $Q_n(i;c)$ に左から $Q_n(i;c^{-1})$ がかけられていると考えると、 $Q_n(i;c)$ の第 $i$ 行が $c^{-1}$ されるので、単位行列となる。即ち

$Q_n(i;c^{-1})Q_n(i;c)=E$

従って、

$Q_n(i;c)Q_n(i;c^{-1})=Q_n(i;c^{-1})Q_n(i;c)=E$

より、 $Q_n(i:c)$ は正則で、その逆行列は $Q_n(i;c^{-1})$ である。

(3) 図３の行列を $R_n(i,j;c)$ とする。

f:id:camelsan:20210127195709p:plain — 図３基本行列三つ目

単位行列の $(i,j)$ 成分( $i\neq j$ )を数 $c$ に変えたものが、 $R_n(i,j;c)$ である。

$(m,n)$ 型行列 $A$ に左から $R_m(i,j:c)$ を掛けると、 $A$ の第 $i$ 行に第 $j$ 行の $c$ 倍が加わる。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, R_2(1,2;2)=\begin{pmatrix}1&2\\0&1\end{pmatrix}$

とすると

$\begin{split}R_2(1,2;2)A&=\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\\&=\begin{pmatrix}1+2\times 4&2+2\times 5&3+2\times 6\\4&5&6\end{pmatrix}\\&=\begin{pmatrix}9&12&15\\4&5&6\end{pmatrix}\end{split}$

従って、 $R_2(1,2;2)$ を左から掛けると、ちょうど $A$ の第 $1$ 行に第 $j$ 行の $2$ 倍が加わっている。

$(m,n)$ 型行列 $A$ に対し、右から $R_n(i,j;c)$ を掛けると、 $A$ の第 $j$ 列に第 $i$ 列の $c$ 倍が加わる。
例：

$A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}, R_3(1,2;2)=\begin{pmatrix}1&2&0\\0&1&0\\0&0&1\end{pmatrix}$

とすると、

$\begin{split}AR_3(1,2;2)&=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\begin{pmatrix}1&2&0\\0&1&0\\0&0&1\end{pmatrix}\\&=\begin{pmatrix}1&1\times 2+2&3\\4&4\times 2+5&6\end{pmatrix}\\&=\begin{pmatrix}1&4&3\\4&13&6\end{pmatrix}\end{split}$

従って、 $R_3(1,2;2)$ を右から掛けると、ちょうど $A$ の第 $2$ 列に第 $1$ 列の $2$ 倍が加わっている。

$R_n(ij;c)$ は正則で、逆行列は $R_n(i,j;-c)$ である。
証明： $R_n(i,j;c)R_n(i,j;-c)$ を考える。 $R_n(i,j;c)$ に右から $R_n(i,j;-c)$ がかけられていると考えると、 $R_n(i,j;c)$ の第 $j$ 列に第 $i$ 列の $-c$ 倍が加わるので、第 $j$ 列の第 $i$ 成分は $0$ となる。即ち単位行列となる。よって

$R_n(i,j;c)R_n(i,j;-c)=E$

$R_n(i,j;-c)R_n(i,j;c)$ を考える。 $R_n(i,j;c)$ に左から $R_n(i,j;-c)$ がかけられていると考えると、 $R_n(i,j;c)$ の第 $i$ 行に第 $j$ 行の $-c$ 倍が加わるので、第 $i$ 行の第 $j$ 成分は $0$ となる。即ち単位行列となる。よって

$R_n(i,j;-c)R_n(i,j;c)=E$

以上の(1)、(2)、(3)の正則行列を基本行列という。行列 $A$ の左または右から基本行列を掛けることを、左基本変形または右基本変形という。両方合わせて、基本変形という。

4. まとめ
基本変形は次の６種類の変形となる。
(左１) 二つの行を入れ替える。
(左２) ある行に $0$ でない数を掛ける。
(左３) ある行に他のある行の定数倍を加える。
(右１) 二つの列を入れ替える。
(右２) ある列に $0$ でない数を掛ける。
(右３) ある列に他のある列の定数倍を加える。

camelsan.hatenablog.com

5. 参考文献
[1] 線型代数入門

線型代数入門（基礎数学） [ 斎藤正彦 ]

価格:2,090円
(2021/12/6 21:07時点)
感想(2件)